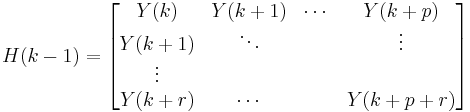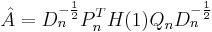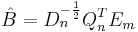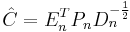Eigensystem realization algorithm
The Eigensystem realization algorithm (ERA) is a system identification technique popular in civil engineering, in particular in structural health monitoring. ERA is a modal analysis technique which generates a system realization using the frequency response given (multi-)input and (multi-)output data.[1]
Algorithm
Given pulse response data form the Hankel matrix
where 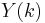 is the
is the 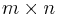 pulse response at time step
pulse response at time step 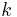 . Next, perform a singular value decomposition of
. Next, perform a singular value decomposition of 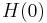 , i.e.
, i.e. 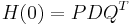 . Then choose only the rows and columns corresponding to physical modes to form the matrices
. Then choose only the rows and columns corresponding to physical modes to form the matrices 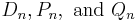 . Then the discrete time system realization can be given by:
. Then the discrete time system realization can be given by:
To generate the system states 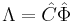 where
where 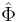 is the matrix of eigenvectors for
is the matrix of eigenvectors for 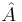 .[2]
.[2]
References
- ^ Marlon D. Hill. "An Experimental Verification of the Eigensystem Realization Algorithm for Vibration Parameter Identification" (pdf). http://mceer.buffalo.edu/publications/resaccom/04-sp06/05Hill.pdf. Retrieved August 24, 2011.
- ^ Juan Martin Caicedo; Shirley J. Dyke; Erik A. Johnson (2004). "Natural Excitation Technique and Eigensystem Realization Algorithm for Phase I of the IASC-ASCE Benchmark Problem: Simulated Data". Journal of Engineering Mechanics 130 (1).